
| with Glaciotectonic Examples
James S. Aber, Professor Emeritus |

| with Glaciotectonic Examples
James S. Aber, Professor Emeritus |
Tectonic movement of lithospheric plates driven by mantle convection gives rise to many structures within the crust. These structures fall into orogenic (mountain building) and epeirogenic (crustal warping) categories depending on the magnitude of deformation. Tectonic structures comprise the majority of features usually dealt with in structural geology.
Many other crustal structures are created by forces which have nothing to do with tectonic movements. Deformations of the crust by meteorite impact, salt-dome uplift, glacier pushing, soft-sediment collapse, landslides, and other mechanisms are important parts of structural geology. These other types of deformations are often considered only briefly in most structural geology lab manuals, but are of paramount significance in many situations encountered by practicing geologists.
This lab manual has a special emphasis on glaciotectonic structures produced by ice shoving, in addition to the more usual geologic structures (Aber 1988). This emphasis should be of particular interest to those living in formerly glaciated areas. Because of their moderate size, glaciotectonic structures are appropriate for beginning students to develop techniques that may later be applied to larger crustal features.
A variety of distinctive structures and landforms are now attributed either wholly or partly to glaciotectonism. Hence, glaciotectonic features must be included with erosional and depositional features as primary field evidence for former glaciation. The modern glacial theory is, therefore, supported by a triad of field evidence, including erosional, deformational, and depositional features—see Fig. 1-1.
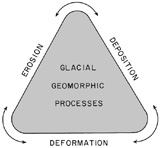
| Figure 1-1. Triad of effects created by ancient glaciation on which the modern glacial theory is based. From Aber and Ber (2007, fig. 1-5). |
Terrain analysis for structural purposes is based on the assumption that landscape topography, drainage, vegetation, and soils often faithfully reflect the nature of subsurface structures. Folds, faults, and other structures are, in fact, often mapped on the basis of topographic expression, even where the bedrock is itself not visible at the surface—see Fig. 1-6.
Several of the exercises are amenable to computer analysis with various software programs. If the necessary software and hardware are available, students are encouraged to work through exercises using both
traditional graphical techniques and computer analysis. Metric
and English units are both used in this lab manual, and students
should become familiar with conversion between the two.
The following materials or equipment are necessary to complete all the lab exercises for this course. Each student should provide the following.
Planar features within rocks include bedding planes and planar cross beds; crystal faces; joints, faults, dikes, fissures and other fractures; veins, foliation, schistosity, cleavage and partings; fold axial planes; seismic discontinuities; water table; formation and other stratigraphic boundaries; and unconformities.
Linear features within rocks include striations, grooves, troughs and channels; yardangs; axes of pebbles, shells, augens, and of other elongated objects; crests of ripples, dunes, drumlins, and of other elongated sedimentary forms; crystallographic and optic axes of minerals; lineations; intersections of fractures or other planar features; fold axes; paleomagnetic axes; rotation axes of plates; strike and dip lines; and lineaments.
The house roof shown in Figure 2-1 illustrates strike and dip in a tilted plane. The horizontal crest of the roof represents the strike with a compass direction of 50° (or N50E). The dip direction of the roof is SE, perpendicular to the strike: 50 + 90 = 140° (or S40E), and the dip angle measured from horizontal is 30°.
The "T" symbol shown on Figure 2-1 is used to indicate
strike-and-dip measurements on maps and diagrams. The long
cross-line represents strike, and the shorter stem represents the
dip direction. The dip angle is sometimes given next to the dip
line. Variations of the basic strike-and-dip symbol are used for
different planar features—see Fig. 2-2.
One common situation involves three nearby wells drilled
into the same tilted horizon. The orientation of that horizon
may be easily calculated and projected into the surrounding area.
The same procedure could also be applied to surface outcrops or to
a combination of surface and subsurface control points. Note
that deep subsurface elevations are often below sea level, and so
are negative.
Figure 2-3 shows a map view of three points for which the
elevations of a distinctive bed are known. The three points are
labelled as follows: A = low point, B = intermediate point, and
C = high point. In this special case, B and C are equal in
elevation. To find the strike and dip, first connect the three
points with straight lines forming a triangle.
Consider, for example, a vertical, E-W cross section through
the house of Figure 2-1. The section cuts diagonally across
the roof, which appears to dip in the section at an angle
less than 30°. Another cross section running parallel to
strike (50°) would show no dip; the roof would appear horizontal. The relationship between true dip and apparent dip is defined by the following functions:
where:
Organization of exercises
Most exercises in this lab manual involve actual geological
examples from North America and northern Europe. This case-history approach seems preferable to made-up exercises that may bear little relationship to real geology. Because of the use of actual situations, some exercises do not have a single right solution. Multiple correct answers are possible in some cases, and the
student would have to use some judgement in selecting the most
reasonable possibility given the data at hand. Far from being a
drawback, this is a more realistic representation of the daily
work of structural geologists.
References
2. PLANAR STRATA
Geometric elements in structural geology
Geologists must deal with structures developed on all scales
from microscopic to continental within all manner of materials
from loose sediments to high-grade metamorphic complexes. Some
of these structures are geometrically simple, but many are
irregular and complex in form due to multiple phases of
deformation. All structures, regardless of their complexity, may
be reduced to combinations of two basic geometric elements—planes and lines, the orientations of which may be determined. ![]() Geometric elements of structural geology.
Geometric elements of structural geology.Orientations of planes and lines
The orientation of a plane relative to the Earth's surface is determined by two measurements, namely strike and dip. Strike is defined as the compass direction of a horizontal line in the
plane. Compass directions are customarily measured in degrees
from 0 to 360°, or could be recorded as N50E, N45W, S15E, etc. Dip
is the direction and angle of maximum downward tilting, which is
always perpendicular (90°) to strike.
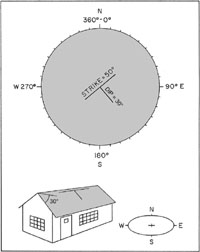
Figure 2-1. Schematic diagram of a house roof (below) with
a strike-and-dip symbol and compass diagram (above).
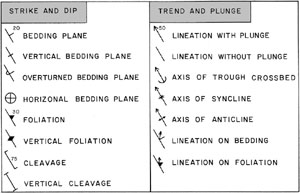
Figure 2-2. Geologic symbols for planar
features (left) and linear features (right).
Finding the orientation of a plane
Geometrically, any three points, which are not in the same
line, define a plane. Given a recognizible planar feature, such
as a marker bed or mineral vein, the strike and dip of that
planar feature could be determined if its elevation is known at
three points. The elevation control points may be in either surface or subsurface locations.
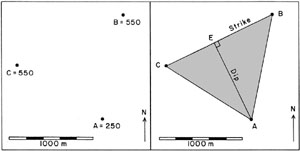
Figure 2-3. Map of sample three-point problem.
Elevations are given for a unique planar feature
(left). Solution for strike and dip shown on right.
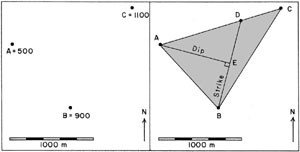
Figure 2-4. Map of sample three-point problem.
Elevations are given for a unique planar feature
(left). Solution for strike and dip shown on right.
Apparent dip and true dip
The true or maximum dip angle is measured only perpendicular to the strike line, as shown by the house roof (Fig. 2-1). A dip angle measured in any other direction would be less than true dip and is called apparent dip.
Note: apparent dip is always less than true dip, which is the maximum dip possible on a tilted plane.
Problem
The large-scale map shows three control points on a distinctive mineralized vein, which outcrops in a roadcut at the eastern point and has been encountered below hills in drill holes to the west—see Fig. 2-5. The vein is assumed to be planar and is of considerable economic interest, as it is known locally to contain malachite, an indicator for possible gold or other valuable metals. 3. PRIMARY STRUCTURE
Introduction
Primary structures are those features created in a rock at the time of its original deposition (sedimentary), cooling (metamorphic), or solidification from magma or lava (igneous). Such features are part of the rock body from its genesis. Recognition of primary structures is important to distinguish from later structures caused by stress, strain, and the resulting deformation of the rock body. ![]() Primary structures.
Primary structures.Problem
The Dakota Formation of middle Cretaceous age in north-central Kansas is famous for its cross bedding. The Dakota was deposited in various coastal, deltaic, and shallow marine environments—see Fig. 3-1.
![]() Table 3-1. Cross-bedding vector data in azimuth degrees. Adapted from Franks et al. (1959, Table 1).
Table 3-1. Cross-bedding vector data in azimuth degrees. Adapted from Franks et al. (1959, Table 1).1. 82 2. 54 3. 53 4. 54
5. 70 6. 95 7. 142 8. 113
9. 174 10. 92 11. 169 12. 175
13. 164 14. 117 15. 133 16. 131
17. 137 18. 167 19. 136 20. 149
21. 175 22. 174 23. 121 24. 233
25. 236 26. 216 27. 233 28. 222
29. 212 30. 219 31. 202 32. 265
33. 203 34. 204 35. 199 36. 270
37. 206 38. 221 39. 230 40. 239
41. 231 42. 236 43. 268 44. 186
45. 192 46. 205 47. 235 48. 260
49. 199 50. 252 51. 215 52. 267
53. 210 54. 290 55. 294 56. 297
57. 284 58. 315 59. 274 60. 273
61. 274 62. 280 63. 291 64. 326
65. 340 66. 306 67. 270 68. 275
69. 290 70. 305 71. 320 72. 325
73. 298 74. 321 75. 282 76. 305
77. 282 78. 279 79. 316 Lab procedures
![]() Table 3-2. Paleocurrent patterns of deposition.
Table 3-2. Paleocurrent patterns of deposition.Environment Local current vector Regional pattern
Alluvial, braided unimodal, low variability diverging
Alluvial, meandering unimodal, high variability converging
Delta unimodal, high variability radiating
Aeolian uni-, bi-, or polymodal large arc
Shore line/shelf bimodal (tides) or other 90° or parallel
to coast line
Continenal slope unimodal (turbidites) radiating References
![]()
![]() Return to Table of Contents.
Return to Table of Contents.